传说在加勒比海上海域被各大海盗集团霸据，海盗之间时常发生冲突，不少集团为了避免被敌对集团消灭，选择联合其他海盗，当然朋友的朋友也是朋友即如果海盗A与海盗B联合，海盗B与海盗C联合，则海盗A与海盗C也为联合关系。我们此时将海盗A,B,C划入同一势力。ghx决定下海一统所有海盗，于是他准备先调查这片海域上有多少势力，他打开了卷轴，卷轴上将各大海盗进行了编号，而且留下了一串奇怪的代码，传说只有将代码空白的部分填写完成即可得到答案，现在将问题简化就是下面的描述。

本题:

给出一个无向有环的非联通图，请你使用DFS算法计算图中的连通分量个数。（虽然你也可以使用BFS，并查集等方法）

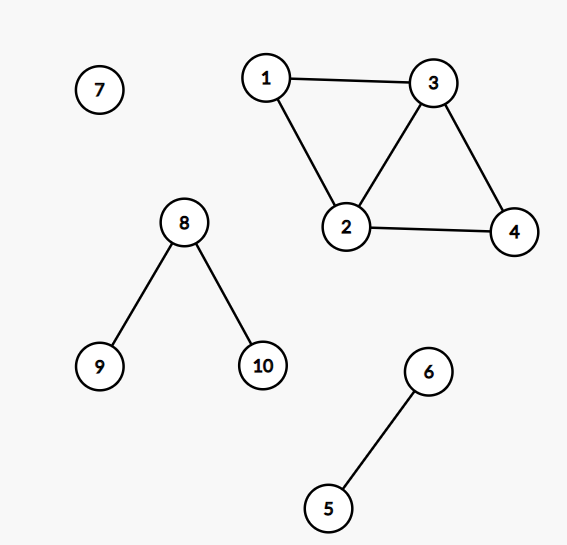
    显而易见，这个图中的连通分量个数为4

当然这题只需要你实现深度优先遍历函数。

请你提交代码中空缺的函数。

下面是部分代码

C/C++:

#include <stdio.h> 
const int N = 1e3 + 10; 
int map[N][N]; 
bool vis[N]; 
int n, m, cnt; 
/* 
       函数 
*/ 
int main() 
{ 
       scanf("%d%d", &n, &m); 
       for (int i = 1; i <= m; i++) 
       { 
              int u, v; 
              scanf("%d%d", &u, &v); 
              map[u][v] = 1; 
              map[v][u] = 1; 
       } 
       for (int i = 1; i <= n; i++) 
       { 
              if (!vis[i]) 
                     dfs(i), ++cnt; 
       } 
       printf("%d\n", cnt); 
       return 0; 
} 


Java:


import java.util.Scanner; 


public class Main 
{ 
    static int N = (int) (1e3 + 10); 
    static int[][] map = new int [N][N]; 
    static boolean[] vis = new boolean[N]; 
    static int n, m, cnt; 
    /* 
        函数 
    */ 
    public static void main(String[] args) 
    { 
        Scanner cin = new Scanner (System.in); 
        n = cin.nextInt(); 
        m = cin.nextInt(); 
        for (int i = 1; i <= m; i++) 
        { 
            int u, v; 
            u = cin.nextInt(); 
            v = cin.nextInt(); 
            map[u][v] = 1; 
            map[v][u] = 1; 
        } 
        for (int i = 1; i <= n; i++) 
        { 
            if (!vis[i]) 
            { 
                dfs(i); 
                ++cnt; 
            } 
        } 
        System.out.println(cnt); 
    } 
}